|
俗话说：眼看他起高楼，眼看他宴宾客，眼看他楼塌了。我想这句话放在我们做技术的，也很合适 —— 基础不牢，地动山摇。 尽管我们很多人不是做基础开发的，但是操作系统、数据结构和算法、计算机网络、设计模式 …… 这些 IT 领域的基础性学科，对于我们来说其实挺重要的。 本文将尝试从理性结合感性的角度去说明为什么计算机用补码存储数据，当我们明白这个问题后，那么，我们就可以去理解另一个衍生问题 —— 数据溢出。我们先来看一段关于数据溢出的 Java 代码片： /* int是有符号数，32位存储，表示范围是－2^31~2^31-1（即－2147483648～2147483647）*/
int i = Integer.MAX_VALUE; // i为2147483647
i += 1; // 加1后，引起数据溢出，则i为－2147483648 加法器 计算机只有加法器没有减法器，两个数的减法运算会被计算机转换为加法运算。 模、补数 在日常生活中，有许多化减为加点例子。我们以最平常的钟表为例，时针逆时针拨 x（0<x<12）格和时针顺时针拨12-x格，效果是相同的。比如，时针从10点调整到5点有以下两种方法： 总结，x + (MOD - x) = MOD 就是模，x 和 MOD - x 就是一对“互补”的数，即原数 x 的补数为 MOD - x 或者原数 MOD - x 的补数为 x。通过对钟表拨时针的例子可以发现，用补数（7）代替原数（5），可把减法转变为加法（出现的进位就是模，进位舍弃）。 二进制数的模，先来看下两个个例子（此处我们忽略符号）： 通过对上面两个例子可以推论：一个二进制数的最高位位数用n表示，那么该二进制数的模就是2^n。 原码、反码、补码 给定一个有符号数 x，对原码、反码、补码的表示： sign and magnitude representation（原码）：最高位位符号位（0表示正数，1表示负数），剩余位（数据位）为 x 的大小。
例如：[+1] = [0000 0001]原，[-1] = [1000 0001]原 ones' complement representation（反码）：如果 x 为正数，则是其二进制表示；如果 x 为负数，则是其对应正数的 bit complement/bitwise NOT（按位取反）—— 执行每一位逻辑否定的一元操作。
可用公式表示为：[x]反 = (2^n - 1) - |X|（其中 n 为将符号位算在内的位数，|X| 为绝对值）
例如：[+1] = [00000001]原 = [00000001]反，[-1] = [10000001]原 = [11111110]反 two's complement representation（补码）：如果 x 为正数，则是其二进制表示；如果 x 为负数，则是其对应正数的二的补（所有位取反后加1）。
可用公式表示为：[x]补 = (2^n) - |X| ＝ [x]反 + 1（其中 n 为将符号位算在内的位数，|X| 为绝对值）
例如：[+1] = [00000001]原 = [00000001]反 = [00000001]补，[-1] = [10000001]原 = [11111110]反 = [11111111]补
计算机为什么用补码存储数据 以4位存储表示有符号数为例，通过原码、反码和补码的表示法来生成一张表： | 有符号数（十进制） | sign and magnitude representation（原码） | ones' complement representation（反码），[x]反 = (2^n - 1) - \X\ | two's complement representation（补码），[x]补 = (2^n) - \X\ |
|---|
| +7 | 0111 | 表示方式不变 | 表示方式不变 | | +6 | 0110 | 表示方式不变 | 表示方式不变 | | +5 | 0101 | 表示方式不变 | 表示方式不变 | | +4 | 0100 | 表示方式不变 | 表示方式不变 | | +3 | 0011 | 表示方式不变 | 表示方式不变 | | +2 | 0010 | 表示方式不变 | 表示方式不变 | | +1 | 0001 | 表示方式不变 | 表示方式不变 | | +0 | 0000 | 表示方式不变 | 表示方式不变 | | -0 | 1000 | 1111 | 0000（求解过程：[x]补 = 2^n - \x\ = 2^4 - \-0\ = 2^4 - (+0)，使用二进制则为10000 - 0000 = 10000，超过4位（有进位），那么舍弃进位1，最终结果就是0000） | | -1 | 1001 | 1110 | 1111 | | -2 | 1010 | 1101 | 1110 | | -3 | 1011 | 1100 | 1101 | | -4 | 1100 | 1011 | 1100 | | -5 | 1101 | 1010 | 1011 | | -6 | 1110 | 1001 | 1010 | | -7 | 1111 | 1000 | 1001 | | -8 | 超出4个bit所能表达范围 | 超出4个bit所能表达范围 | 1000 | | 备注 | 零重码，二进制存在两种表示方法：0000和1000 | 零重码，二进制存在两种表示方法：0000和1111 | 零无重码，同时解决了原码和反码不能表示-8的问题 |
通过上述表格，可以很自然的总结出一个结论：补码表示法（two's complement representation）可以防止0的机器数重码，同时又解决了原码和反码无法表示－8的问题，这样就极大的简化了计算机的硬件设计。 结合之前提到的时钟例子，我们把补码表示法（two's complement representation）所表示的四位存储单元，按照从0000到1111递增的方式，均匀的分布在时钟的表盘上。于是，我们就可以得到下面这张图：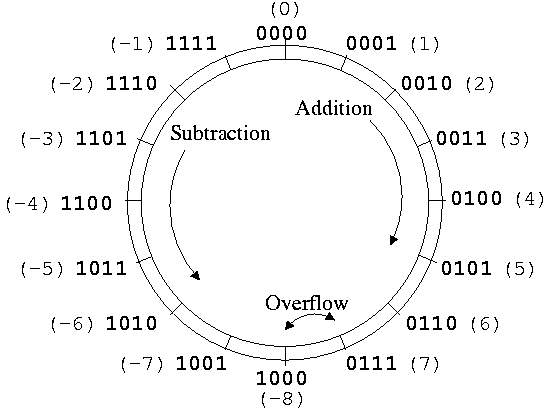 
继续以时钟的方式来观察上图： 顺时针方向位加法，逆时针方向为减法 模为2^n：在1111处顺时针拨一格，就到了0000。用数学的方式，即1111 + 1 = 10000，进位舍弃则结果为0000，那么四位存储的模就是10000（2^4） 减法转换为加法：3 - 1 = 3 + （-1） = 0011 + 1111 = 0010，眼尖的人可能会说0011 + 1111明明等于10010，怎么会是0010？还记得之前提过的最高位进位舍弃嘛，因此对于4位存储来说，进位舍弃后就是0010 = 2。 数据溢出：当0111（7）加1时，按照我们人的思维来说，应该结果为8，但是对于机器来说则不是，因为0111（7）是四位存储所能表示的最大有符号数，所以它是无法表示01000（8）的，这个时候我们就说数据溢出了。那么数据溢出该怎么办呢？很简单，机器的思考方式显然和我们人脑不一样，机器按照上面环形图的方式，由于0111（7）加1是顺时针造成的数据溢出，那么我们可以把机器的操作想象成在0111（7）处顺时针拨了一格，我们再去对照下环形图发现这时候指向了1000（－8）。
至此，我们完全可以总结一下，并解答计算机为什么用补码存储数据：
Reference http://www.jianshu.com/p/63cc96758d20
转载请并标注: “本文转载自 linkedkeeper.com ” ©著作权归作者所有
|
